由于历史原因,传统的有限元分析对象主要是基于结构力学的模型,只在较小范围内涉及传热。随着多物理场仿真应用的日益增加,有限元法在流体流动和电磁仿真中得到了广泛应用,“有限元分析”一词也逐渐被其他工程和科学领域所接受和认可。事实上,无论是在何种应用领域,有限元分析过程都是相同的。
下面简要概述有限元分析的主要工作流程,涵盖从几何到模型文档的各个过程。
几何
有限元分析要求模型几何“紧密相连”。计算机辅助设计(CAD)几何结构并不总是用于分析目的。举个例子,现实生活中的某个物体可以通过 CAD 绘图中一组松散连接的三维表面来描述;然而在有限元分析中,这些表面必须能够形成一个真实的体。
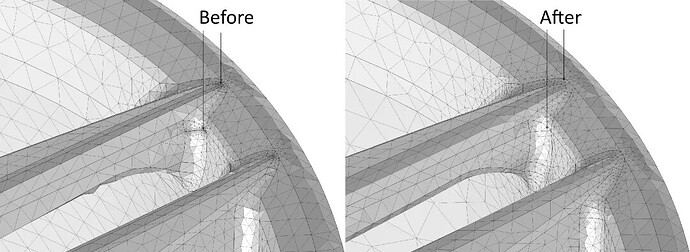
即使 CAD 绘图中的一组三维表面能够形成一个体,但很可能存在一些表面过于细长,而一些边对于几何尺寸而言又过短的情况。这样一来,这些不理想的几何特征上便会产生不符合要求的单元分布。
为了准备一个可用于有限元分析的 CAD 几何,通常需要对几何进行修复和特征去除。修复操作可以修补几何中不“紧密相连”的部分,特征去除操作可以移除细长表面或合并多余的小边。
为了进行分析而创建、修复 CAD 几何以及去除特征的过程,通常是更大过程的一个环节——在有限元分析中,传统上称之为预处理。
材料
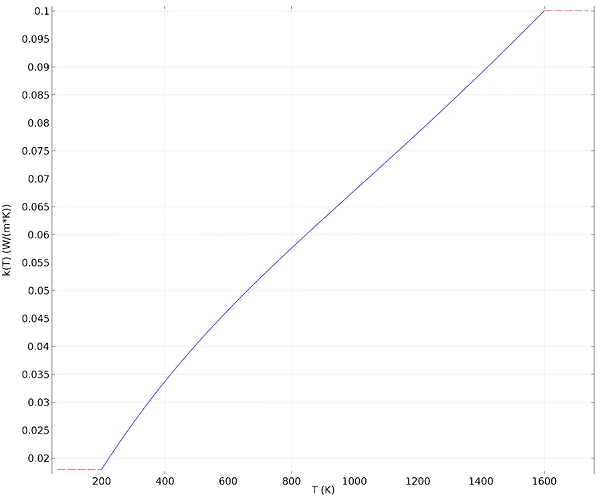
数学模型中的本构关系涉及材料的物理属性,这些属性可能与模拟变量(“因变量”)相关。例如,在热膨胀分析中,机械属性和热属性往往与温度相关。
空气导热系数随温度的变化情况。
在实际操作中,需要正确估计材料属性和参考点的有效间隔。除此之外,还必须为几何的各个部分指派不同属性的材料。
在传统的有限元分析中,定义和指派材料属性及材料属性函数的过程,通常也认为是预处理的一部分。
域设置、边界条件、载荷及约束
在结构力学中,通过为系统选择的材料、载荷及约束可以定义数学模型。一般情况下,设置材料、域方程、边界条件和初始条件,即可定义数学模型。
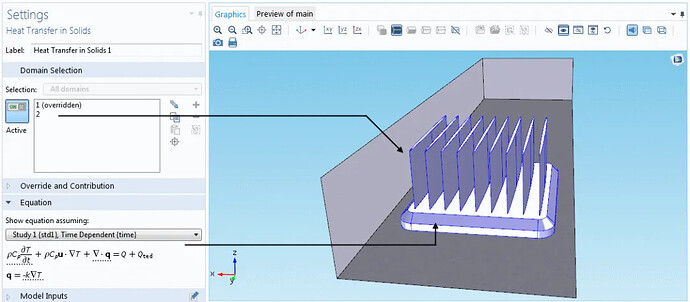
通过选择固体传热接口,可自动定义散热器中的域方程。方程描述包含温度相关属性。通过显示这些方程,您可以了解模型背后的原理。
这部分的分析涉及选择几何域、边界、边和点,以及为这些几何实体指派方程、载荷或约束。这些设置的定义过程通常也认为是传统有限元分析中预处理的一部分。
网格
几何、材料、域设置、边界条件、初始条件、荷载及约束的定义无需离散化即可进行。然而,在许多较早的有限元分析软件中,仍然是基于离散模型来执行这些操作的。
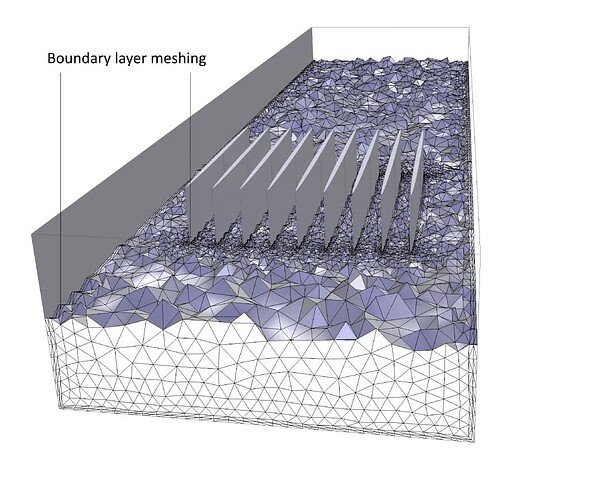
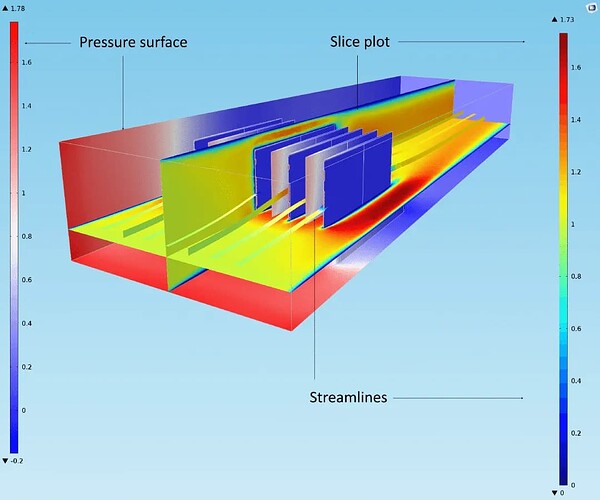
网格创建完成后,我们便得到一个完整的数值模型。不同的现象和分析需要使用不同的网格设置。例如,在波的传播问题(例如,结构力学中的弹性波建模,或者射频分析中的电磁波建模)中,最大单元的尺寸必须远小于波长才能正确求解问题。在流体流动中,可能需要边界层网格才能解析边界层,而单元雷诺数可以确定流体本体的单元尺寸。
通过适用于流体流动建模的边界层网格划分方法,对固体表面网格进行细化。
在许多情况下,CAD 几何的不同部分必须单独进行网格剖分。各部分之间界面处的模型变量必须通过有限元分析软件进行匹配,这一操作可以通过连续性约束(即用于将不同部分的有限元离散相互关联的边界条件)来实现。由于这些条件可能具有非局部特性,它们通常被称为多点约束。
在传统的有限元分析中,网格划分被认为是难度最高的预处理任务之一;而在现代有限元分析软件中,初始网格可以在求解过程中自动改变,从而尽可能减小数值解的误差,这种方法称为自适应网格划分。
解
如果说创建网格是一项高难度的任务,那么在合理的计算时间内选择和设置求解器并求得方程的解(构成数值模型)便是一项更加艰巨的工作。这些困难与求解过程中面临的各项挑战紧密相关。
首先,使用代数方程的离散模型可能非常大。一个三维模型往往拥有数百万个自由度。基于有限元法的数值模型求解过程的中心环节,是求解大型线性代数方程组。非线性、参数化、特征值和瞬态问题则通过迭代法求解一系列大型线性方程组来解决。
一般来说,大型线性方程组很难进行有效求解。尽管可以使用现成的黑箱法,但这种方法对于实际模型而言往往代价过高,相关示例包括基于 LU 因式分解法的直接求解器,或通用的迭代法。
为了寻求一个成功且近乎最优的替代方案,必须利用基础系统的某种结构。对于多物理场问题,这种结构可能并不存在,或者难以识别。在这种情况下,一个有用的做法是,将问题按物理成分进行分解,从而使分解的结构能被有效利用。现代有限元分析软件使用几何或代数多重网格法,来加快线性系统的迭代求解过程。
有限元分析求解器的另一个问题来源是模型的非线性。牛顿方法使用局部导数信息来寻求更好的候选解;但只有在当前的估计解与真正的数值解足够接近时,这种方法才可靠。实际上,对解的初始猜测值并不总是与真实值足够接近;在这样的情况下,使用牛顿方法通常无法正确求解。对问题进行不同的简化或放宽可能会有所帮助。通过求解更为简单的相似问题来代替原始问题,可以得到候选解。例如,可以忽略某些非线性来得到一个容易求解的线性问题。为此,我们开发了分离式求解器和连续求解器。
有限元分析求解器遇到的第三类困难,是数值模型可能不稳定,或者由于其他原因,没有为数学模型提供较好的近似。与更完善、性能更优的数值模型相比,这些情况下的求解过程要显得困难得多。我们可能很难发现和理解引起这一问题的根本原因。在许多情况下,我们可以采用某种方式修改模型而不是通过设置求解器作为补救措施。因此,更好的自适应网格通常是模型性能改进的重要组成部分。
总而言之,求解器的设置选项需要非常灵活;同时,还要能调用各种功能强大的方法。我们往往需要在稳定性和性能之间达成折衷。
通过扰乱数值模型来研究其灵敏度,始终是一个很好的做法。这样做可以到达两个相关目的:检查模型是否具有数值上的稳定性,以及对当前有限元分析中的一些重要物理量的截断误差进行量化。有限元离散的截断误差通常(但不总是)决定着仿真中的误差。为此,可以将模型中的关键派生值与典型的网格单元尺寸进行比较,然后采用不同的网格(在理想情况下,采用与当前网格明显不同的其他两个网格,且它们彼此也存在较大差异)重复进行计算。
如果数值模型性能良好,便可以根据比较结果估计精度阶数。如果精度阶数为正数,则所研究的两个最精细网格之间的物理量的差值,可以作为该物理量的截断误差估计值。有时,我们很难创建出满足所有需求的多个网格;在这种情况下,需要使用两个截然不同的网格的比较结果作为替代方法。
如果差值较小,表明该数值模型表现良好,且这个物理量的截断误差也较小。但是,如果差值较大,则很难得出任何结论。这种差异可能是由于两个网格的不稳定性或精度低造成的。然而,细化网格的解可能是精确的,而粗化网格的解则可能精度较差。即使截断误差估计尚不确定,至少可以排除模型不稳定的风险(例如,使用与该细化网格相当但不同的其他网格)。其他离散参数和求解器设置(如容差)也应进行更改。如果对于所有“扰动”仿真来说,研究的物理量只发生了很小程度的变化,则说明该数值模型具有良好的稳定性。
结果
对数值求解器的计算结果进行的分析包括:研究建模场的三维绘图、横截面图(如 x-y 绘图)以及计算派生值,例如对体、表面或边求积分,或计算沿边或点的表达式的值。
在较早的有限元分析软件中,必须先定义要分析的绘图和派生值,才能进行求解。如果遗漏某些关键定义,则意味着需要从头开始重新求解。因此,定义要在后处理过程中分析的表达式和派生值,也认为是预处理的一部分。
现代有限元分析软件支持在计算出解之后,动态定义表达式和派生值。在这些软件中,表达式和派生值的定义是后处理的重要组成部分,用于对模型进行深入预测。
基于表达式和派生值生成三维绘图、表面图、x-y 绘图和表格值,然后进行分析,是正确的后处理操作。
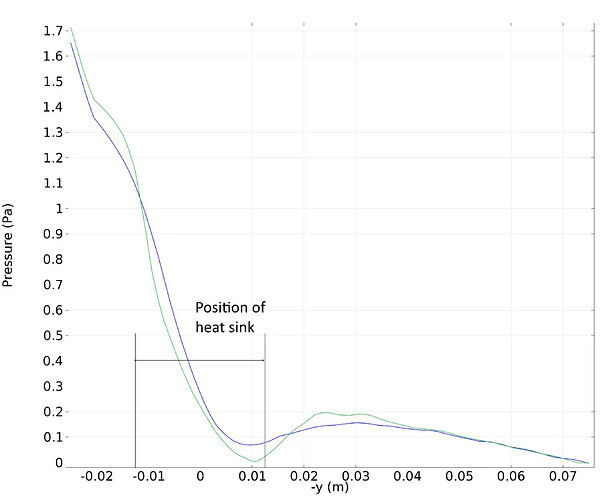
翅片顶部(蓝色)和底部(绿色)沿流动方向的压力损失。由于流体必须通过横截面相对较大的散热器底座,因此底部的压力损失略大一些。
后处理中的一项重要任务是估计数值解中的误差。如上所述,可以通过求解不同网格尺寸的数值模型方程,来估计数值解的收敛性,从而实现误差估计。
后处理的另一个重要部分是估计模型对不同数据(如材料属性、初始条件、边界条件、载荷、约束以及数学模型和数值模型所需的其他输入参数)的灵敏度。
自动生成模型文档
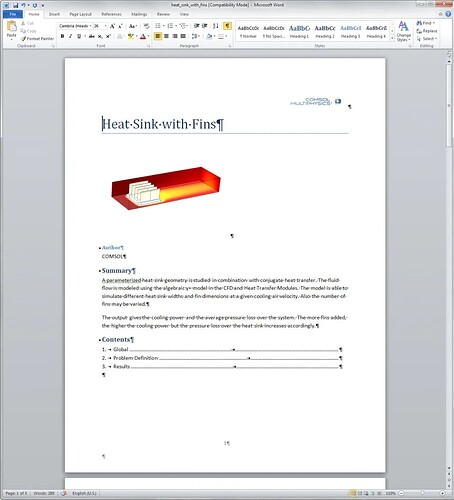
在运行仿真后,非常重要的一步是将输入数据和仿真结果汇总到报告中,并在其中记录特定的会话。现代有限元分析软件支持定义报告的结构,用户可以在其中选择要记录的输入和输出数据。系统可以自动生成此类报告,您可以将其另存为文档,在将来每次仿真时作为参考使用。
散热器仿真报告的第一页。创建完成报告结构后,便会根据每次仿真结果自动更新报告,并能以不同的名称进行保存,以记录仿真信息。其中包含一个问题定义部分,记录域设置、边界设置、初始条件、网格、自由度数量等信息。结果包含派生值和模型文件中的绘图。