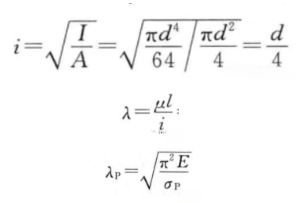相似的文章可参考Workbench 屈曲分析步骤之一
什么是屈曲
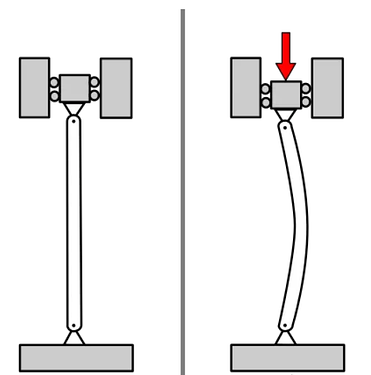
杆件的设计需要特定的强度与偏转要求,且也需要有保持稳定承载的能力。而一些细长杆件的设计,稳定性要求是极其重要的,尤其是承受足够大的压缩载荷时,可能会引起杆件突然的横向或者侧向偏转。这类杆件是圆柱,而出现的横向或者侧向偏转称之为屈曲。
细长杆屈曲只是其中一个对象,还有许多结构可能出现屈曲,如薄板、圆环、薄壳等。它们共同特征就是一般受到压缩载荷,几何为细长或薄壁件。如果结构比较复杂,那么可能出现局部屈曲,也可能结构整体发生屈曲。
从上面可知,屈曲对应的是结构稳定性,但是结构的稳定性并不是只有屈曲这一种。如横梁受到偏心载荷,出现侧向失稳,这与屈曲是不同的。所能承受最大接近屈曲的轴向载荷称之为临界载荷。但是实际结构由于不是理想的,如存在着微观材料缺陷、宏观裂纹,以及非线性等因素,导致尚未到达临界载荷时结构就已经发生了屈曲行为。
线性屈曲
屈曲有很多种,线性屈曲是线性屈曲中最基础的一种。就好像在梁的弯曲中,由纯弯曲了解梁结构是同样的思路。屈曲还分为非线性屈曲,即屈曲的结构引入了非线性因素,临界屈曲载荷与抗弯刚度便不再是线性关系了。至于什么是非线性,有哪些非线性不是我现在想要关心的。线性屈曲即正好对应材料力学经典欧拉杆计算,因此它的限制条件十分明显。
线性屈曲分析有一些限制条件:
(1)做的是线性分析,因此不引入非线性因素,如非弹性本构、大变形、大偏转等;
(2)做的是静态分析,结构需要约束住所有自由度,不得有刚体位移。
上面为屈曲分析所对应的问题描述,这里是线性屈曲分析,故对应的K与S都是常量矩阵。在这个方程中,{Ψi}为屈曲是某一阶特征向量,即所谓的屈曲模态。因为屈曲刚发生(临界),所以已经存在着该项。只能是下面这一项为0,求解该方程即获得特征值和对应的特征向量,特征值也称载荷因子。
\left [ K \right ] +\lambda _{i} \left [ S \right ]
分析流程
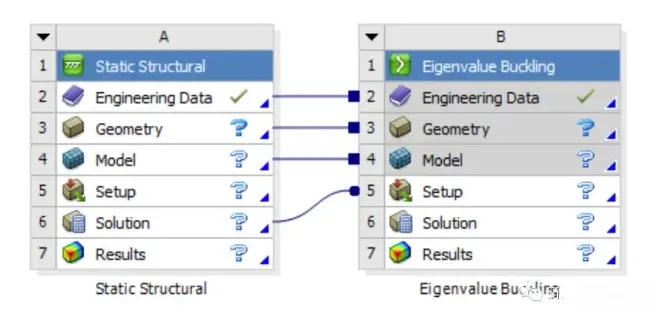
最基础的分析流程如下所示:
首先建立一个结构静力学分析模块,然后将特征值分析(新版本改为Buckling Analysis)拖到静力学分析结果之前,流程建立完毕。在静力学分析模块建立模型以及详细的边界条件,至于载荷的施加通常是有两种方法,现有资料显示:
(1)对结构施加实际大小的载荷,即前面就是一个完整实际的静力学分析,接着将材料至分析结果都传递给屈曲分析,不需要再在屈曲里面改变边界条件以及载荷,直接求解,变得到了载荷因子,将载荷因子乘以实际载荷即得到屈曲载荷,此屈曲因子相当于安全系数。
(2)施加单位载荷(载荷大小为1),其他与方法(1)一样,求解得到的是载荷因子就是屈曲载荷值。
经过屈曲分析,可以得到的有:屈曲载荷和屈曲模态。要让结构产生屈曲,载荷可以有许多,可以说屈曲载荷是属于一个范围(区间)。
而通常只关心最小的屈曲载荷,这个是很容易理解的,因为它是设计的下限值,就好像强度设计要求某个应力最大的截面一样的。每一个载荷因子都对应一个特征向量,因此也倾慕于最小载荷因子所对应的特征向量。但并不是不关心其他更高阶的载荷因子或者屈曲模态。只是这里想要与欧拉压杆相对应,所以特别指出关注低阶。
实际分析中既要观察低阶,也有可能关注高阶,通常是给定一个范围获取。如在用杆单元模拟悬索与实体混合建模的时候,如果对其进行屈曲分析,由于悬索柔度比较大(相对于一些实体),所以低阶的模态基本上都是悬索,需要更多高阶模态才能反映出屈曲情况。如果只关注最低阶,而不是一个范围,可能就忽略了特征值排列的一些特征,从而忽略了对结构一些重要的判断,如密排的特征值预示结构对于缺陷很敏感,需要更多高阶模态以及后续做一些相关的非线性分析来综合判断结构。
分析实例
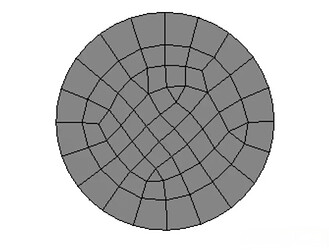
首先在DM里面建立一个实体圆柱,长度200mm,直径10mm,采用软件自带的线弹性结构钢,划分网格得到如下结果:
最终求的是特征值与特征向量,这么说可能不是十分明显。特征向量就是常讲的屈曲模态,反映出来的是可能的变形分布。说白了,最后求出来是个位移值,而一开始有限元理论提到,位移的形函数是固有连续的。因此从位移值分布的连续性上讲,屈曲模态的求解精度对于网格要求相对于应力解要低,也就是同样的网格可能屈曲模态会得到较好的精度的结果。这里几何形状简单,我们指定圆环划分分数为20等份,很容易获得上面的网格。
边界条件
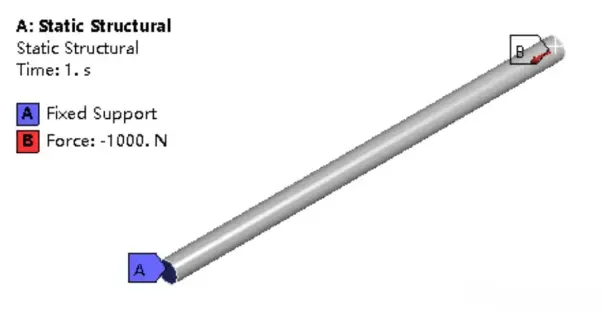
方法一
施加一端端面固定(Fixed),一端施加轴向集中力1000N,这里给的是实际载荷。
求解结果
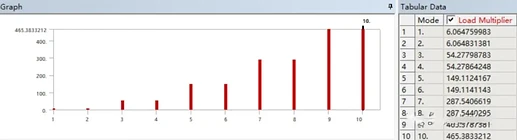
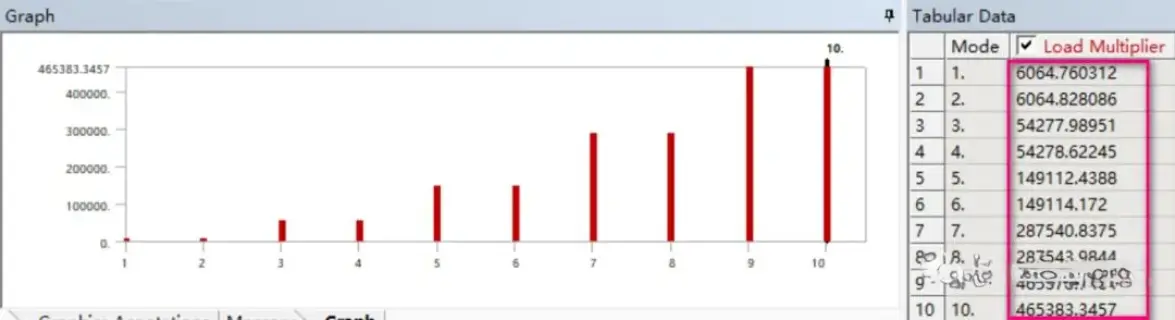
直接对屈曲分析求解,无需任何设置,默认是提取前两阶屈曲模态。给定的阶数越多,计算时间越长,个人设置求解10阶。
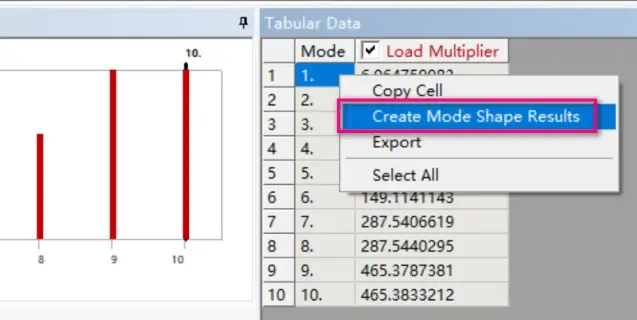
点击屈曲屈曲分析的结构【Solution(B6)】,可以从软件图形窗口下侧查看到这么些信息。最右侧的表格展示出了前10阶对应的载荷因子,如果需要查看某一阶屈曲模态,只需要用鼠标选择表格对应的阶,然后单击鼠标右键,选择【Create Mode Shape Results】即可创建,也可选择所有的,数据同样可以导出。
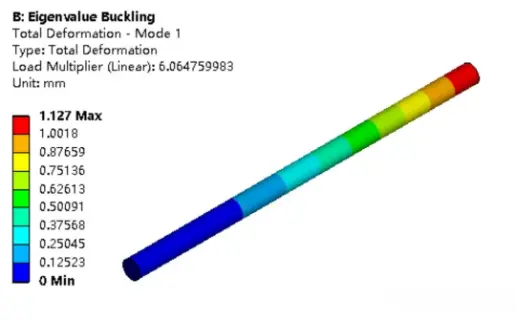
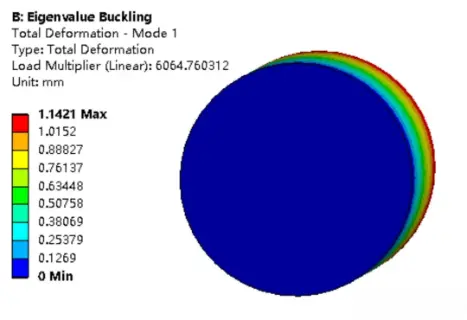
查看一阶屈曲模态分布情况:
上图显示,最大位移分布相对趋势。在固定端及其附近有最小位移,相对于结构其他部分。载荷施加处有相对于其它位置最大位移,为1.127mm。这里显示的位移大小表示各部分的相对分布趋势,即在屈曲开始时,不可用于实际评判,数据不是绝对的。
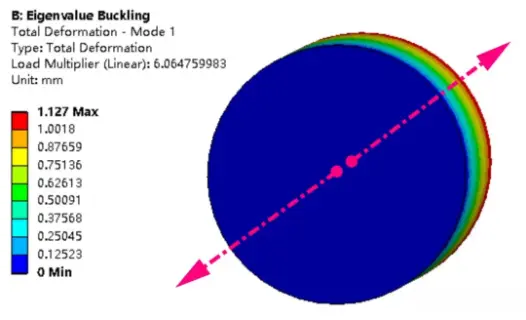
观察动画发现,结构沿着上图双向箭头的方向摆动,约XY平面内一三象限,XY角平分线方向。根据前面给出的计算方法,如果给定的是真实载荷,得到的就类似于安全因子的载荷因子,则临界屈曲载荷大小为:施加真实载荷大小乘以载荷因子:1000N*6.064759983=6064.75983N。
方法二
将上面的真实载荷修改为1N的单位压缩集中力,其余部分保持不变,重新进行求解,可得到如下表格:
观察发现载荷乘子,全部都发生变化了,全部扩大了1000倍。前面提到方法中,如果施加的是单位载荷,获得的刚好就是临界屈曲载荷。这个与删改你施加实际载荷计算几乎一致。查看下屈曲模态:
观察动画就会发现,与前面施加真实载荷完全一致。
欧拉压杆计算
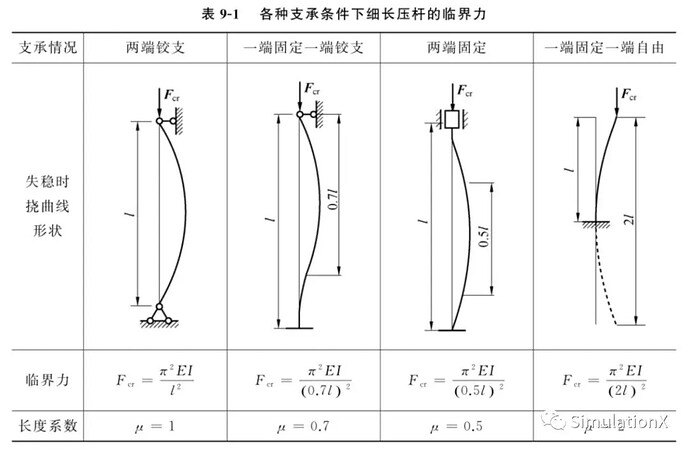
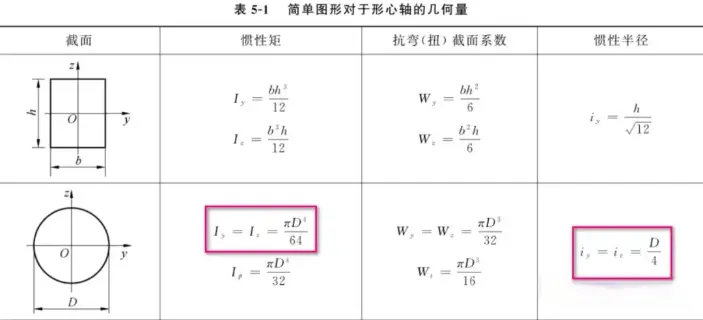
整个几何长度200mm,直径10mm,弹性模量2.0e11Pa。根据欧拉计算公式,参考下表:
圆的惯性半径为d/4,可以计算柔度为160。
Q235柔度为100,钢材弹性模量相差无几,ANSYS自带结构钢屈服极限250MPa,姑且认为两者柔度接近。因为计算出柔度160是大于材料比例极限对应的柔度,故满足欧拉压杆条件。根据欧拉压杆临界压力计算公式:
\pi ^{2}\times E\times I/(\mu L)^{2} ,其中I的计算公式为:
π取3.14,经过计算得到临界屈曲载荷6046.708N,计算得到的结果与软件匹配的十分好。