1 前言
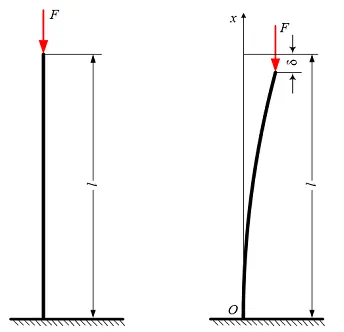
结构失稳即屈曲,最常见的便是压杆失稳现象。压杆稳定示意图如下,在稳定点之前,支反力呈线性增长,逐渐达到一个极值,之后支反力降低,这个极值便是屈曲极限。屈曲极限往往远小于材料的屈服强度,屈曲分析的目的在于找出结构的屈曲极限,分析出结构的安全载荷、或对结构进行相应优化设计提高屈曲极限。
分析屈曲有两类方法:
一类是线性特征值屈曲,用于计算理想线性屈曲极限,
一类是非线性分析,用于计算零件因初始缺陷、材料、几何、接触等引起的非线性屈曲,而非线性分析又分为前屈曲分析和后屈曲分析。
很多结构设计是以理想线性屈曲极限除以一个安全系数作为设计依据,但是如果要探究结构的实际屈曲极限,有必要进行非线性屈曲分析。
特征值模态只是结构的线性特征,是结构在受荷载情况下能量最小的变形模式,不是真实变形。最终采用大变形方法计算得到的结果才是结构真正的破坏状态。
为什么要进行结构屈曲分析?在实际工程问题中,细长压杆、薄壁圆筒、真空容器等细长或薄壁件,一般承受较大的压缩载荷,可能会突然发生曲屈而失去承载能力。
结构不稳定现象
如上图所示的细长压杆,虽然负载基本没有变化,但是任意方向的微小载荷、很小动荡都会使结构有很大改变,出现不稳定现象。因此,需要对该类结构进行曲屈分析,以保证其具有稳定的承载能力。
2 涉及概念
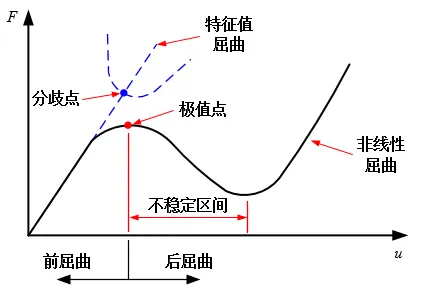
在保守载荷系统下,弹性结构存在两种失稳形式,即分岔点失稳和极值点失稳。荷载-位移全过程曲线,如下图所示。
线性屈曲与非线性屈曲
结构屈曲分析主要涉及以下概念:
(1) 屈曲:当载荷达到某一临界值时,结构将突然跳到另一个随遇的平衡状态,称之为屈曲。临界点之前称为前屈曲,临界点之后称为后屈曲。
(2) 临界载荷:结构在理论上的失稳载荷,所能承受最大接近曲屈的载荷,或屈曲开始时的载荷。
(3) 极限载荷:结构在实际环境中的失稳载荷,扰动和非线性行为使结构在低于临界载荷时就变得不稳定。
(4) 分岔点失稳:第一类失稳。表现为结构的平衡状态出现分岔现象,原有的平衡状态失去稳定性而转向新的平衡状态。基于小变形理论。
(5) 极值点失稳:第二类失稳。结构存在初始缺陷,不再表现为分岔失稳,往往出现变形跳跃,结构的平衡是不稳定的。基于大变形理论。
3 分析技术
曲屈是结构失稳的一种现象,结构稳定性主要采用屈曲分析。曲屈分析主要用于研究结构在特定载荷下的稳定性,以及确定结构失稳的临界载荷,分为线性屈曲分析和非线性屈曲分析。
3.1 线性屈曲分析
线性屈曲分析以特征值为对象,以小位移、小应变的线弹性理论为基础,预测理想线弹性结构的理论曲屈强度,可以得到屈曲载荷和屈曲模态,又称为特征值分析或线弹性失稳分析。
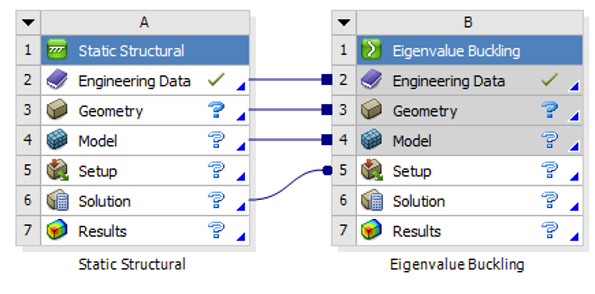
ANSYS Workbench 线性屈曲分析项目流程如下图所示,首先进行结构静力学计算,然后进行线性特征值屈曲计算。将在下篇文章进行详细讲解。
ANSYS Workbench线性曲屈分析项目流程图
线性屈曲分析是线性分析,因此不引入非线性因素,如非弹性本构、大变形、大偏转等。线性屈曲分析是静态分析,需要约束所有自由度,不得有刚体位移。
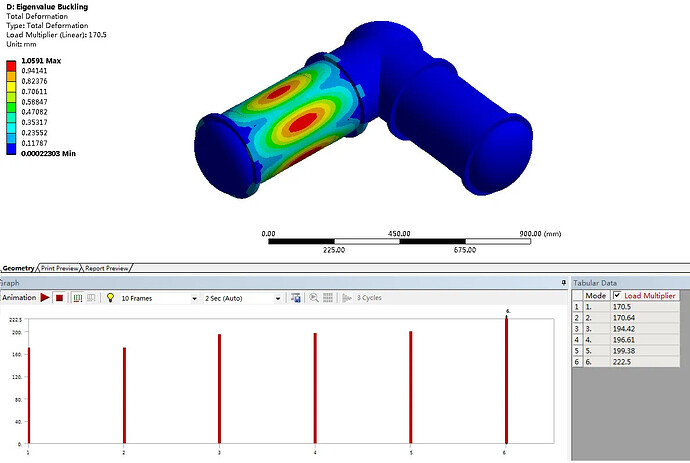
真空容器线性曲屈
线性屈曲分析忽略了微观缺陷、宏观裂纹以及非线性行为,产生不保守的结果,预测值偏高,计算误差较大。但是,求解速度快,计算省时,效率高,可以提供屈曲失效的上限值。
3.2 非线性屈曲分析
在实际结构中,缺陷和非线性行为阻止了系统达到理论屈曲强度。非线性屈曲分析考虑了材料和几何非线性、载荷扰动、几何缺陷和间隙,是一种非线性静力分析。
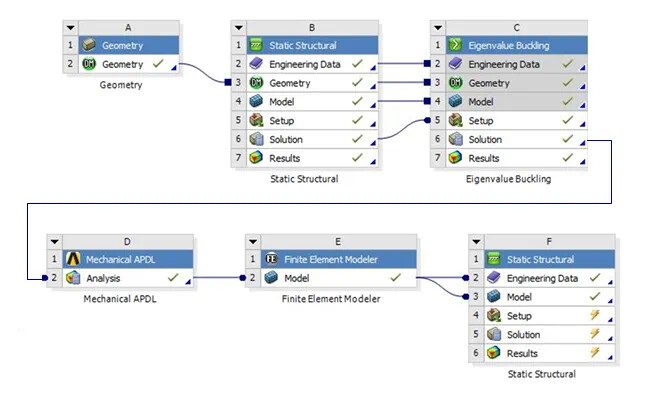
ANSYS Workbench 非线性屈曲分析项目流程如下图所示,主要包括3步:
(1) 进行线性屈曲分析,获得结构屈曲模态;
(2) 施加结构几何初始缺陷;
(3) 进行非线性静力分析。
ANSYS Workbench非线性曲屈分析项目流程图
非线性屈曲分析包括几何非线性失稳分析、弹塑性失稳分析(材料非线性失稳分析)、非线性后屈曲分析(几何非线性和材料非线性)。比较接近实际情况,计算结果更加准确,而且可以进行后屈曲分析。
4 结语
特征值屈曲分析属于线性分析,它对结构临界失稳载荷的预测往往要高于结构实际的临界失稳载荷,因此在实际的工程结构分析时一般不用特征值屈曲分析。但是,特征值屈曲分析作为非线性屈曲分析的初步评估作用是非常有用的。