在有限元分析领域,经常有同仁提出关于网格划分的问题,同时观察到实践中存在一些不合理的网格划分行为,例如对规则实体进行过度划分,以至于网格数量达到上亿级别,这种做法在学术上是不被推崇的。
众所周知,网格划分的精细化程度与分析结果的准确性呈正相关,这是进行网格收敛性研究的主要原因。然而,网格数量的增加不可避免地会导致计算效率的下降,尤其在显式动态分析中更为显著。显式动态分析要求时间步长必须小于某个临界值以确保计算的稳定性,而网格尺寸的减小会降低最小稳定时间步长,同时增加的网格数量也会增加计算负荷。
在单元质量检查过程中,长细比(Aspect Ratio)是一个重要的考量因素。当长细比超过10时,通常被认为是单元质量较差。但是,单元的实际表现还取决于边界条件,因此在某些情况下,长细比较高的单元并不一定导致分析结果的恶化。单元质量检查应被视为一种预警机制,而针对具体问题的分析应结合实际情况进行。
在实际应用中,通常的做法是在应力梯度变化显著或几何曲率变化较大的区域进行更细致的网格划分。此外,需要明确区分两个概念:
-
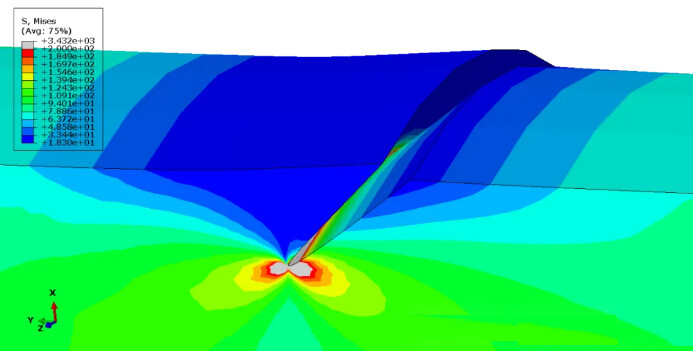
应力奇异:应力奇异是指在数值计算中出现的奇异点,如裂纹尖端或集中力作用点。这些位置理论上无法通过网格细化获得准确结果,过度细化反而可能导致应力预测失真。因此,在这种情况下,应重新评估边界条件的合理性。
-
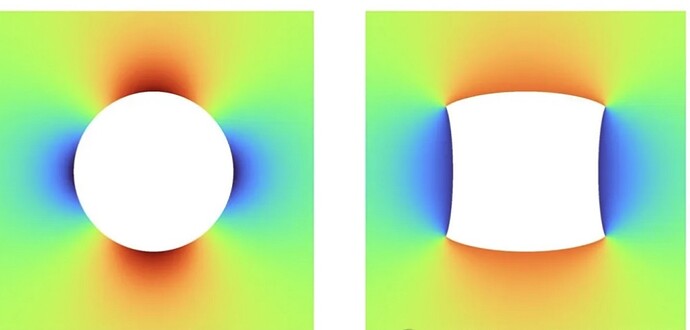
应力集中:应力集中通常出现在几何形状不规则或开孔周围。通过细化网格可以在一定程度上缓解应力集中问题,但应力集中区域的网格应尽可能保持规则性。
选择合适的单元类型对于提高分析效率至关重要。对于实体、壳体、薄膜等不同类型的结构,可以采用精度更高的单元类型。对于螺栓、焊缝等细节部分,可以通过使用RBE(刚性体元素)、梁、线缆等简化单元来减少计算规模,仅在需要详细分析螺栓或焊接区域时采用实体建模(通常采用局部模型)。
最后,强调一点:在进行有限元分析时,不应盲目地一键划分网格,而应先对问题进行深入分析,合理设置边界条件,避免无谓的网格加密。