一、内力的概念
1. 定义
内力,是指由外力作用所引起的、物体内相邻部分之间相互作用力(附加内力)。杆件所受到外界施加的力称为外力。
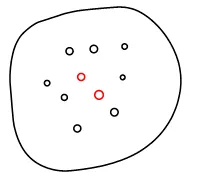
如图所示为任意一个物体,它是由无穷多的微粒组成的,构件内任意相邻两个微粒之间存在着相互作用力,作用力的大小与微粒之间的相对位置有关系。当物体受到外力作用后,物体发生变形,其内部微粒之间的相对位置发生改变,它们之间的相互作用力随之发生改变。我们把这个由外力作用而产生的作用力的改变量称为附加内力,简称为内力。
2. 内力的求法——截面法
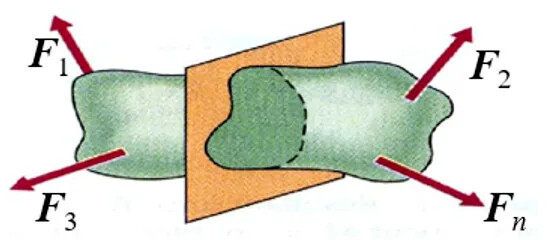
显然内力在构件的内部,想要求解内力,只有让内力暴露出来,这样根据需要求解内力的截面位置,我们采用截面法。假想地把该截面截开,原构件是平衡的,截开后的任意一部分也是平衡的,即截面两侧的任意一部分在外力及截面上的内力作用下处于平衡状态。因此,可以取截面的任意一侧,研究其平衡条件,建立平衡方程,求解该截面上的内力。具体截面求解步骤如下。
- 假想截开: 在所求内力的截面处(一般是横截面),假想地用截面将杆件一分为二。
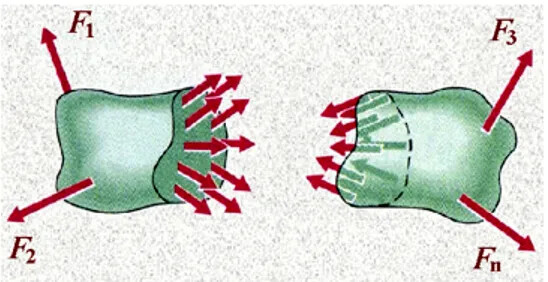
- 代替: 任意取一部分,其舍弃部分对留下部分的作用,用作用在截面上相应的内力(力或力偶)代替。
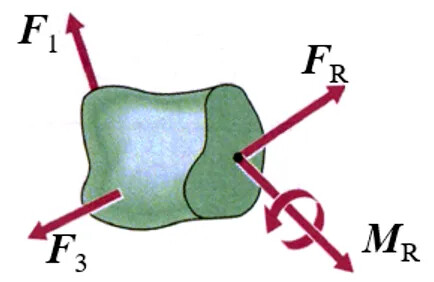
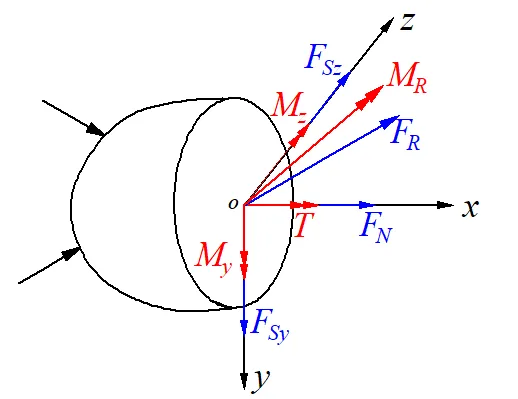
- 平衡: 对留下的部分建立平衡方程,根据其上已知外力来计算杆在截开面上的未知内力(此时,截开面上的内力对所保留部分而言是外力)。根据均匀性连续性的基本假设,截开后的截面上应该是连续分布着一任意力,截面上各点处都有内力,而空间任意力系的平衡条件只有六个,我们求解不出所有各点的内力。根据力系的简化,我们把这个内力的任意力系向截面的一点简化,通常向截面的形心简化,得到一个主矢一个主矩,如下图所示。
以截面形心为原点,建立直角坐标系如图x轴垂直于横截面,即沿杆的轴线方向,y、z轴在截面面内。把主矢向三个坐标轴分解可得三个分量:沿着x轴的轴力,沿着y轴和z轴的剪力。

把主矩向三个坐标轴分解可得三个分量:沿着x轴的扭矩,沿着y轴和z轴的弯矩。
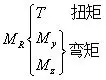
我们把这六个分量也称为内力,但是要注意这六个分量是内力的合力或合力矩。在后面求解杆件的内力,就是求轴力、剪力、扭矩和弯矩,因为这几个内力分别对应着杆件的基本变形:拉伸和压缩变形、剪切变形、扭转变形、弯曲变形。
二、应力的概念
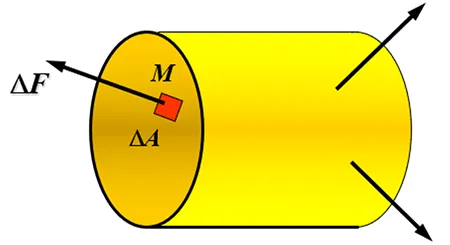
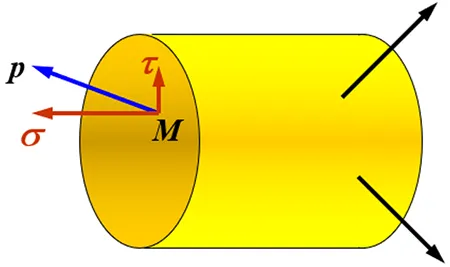
应力是内力的分布集度(应力是针对某“点”而言的,我们要描述一点的应力时,应该指出这个点的位置及过这个点的平面的方位),为了描述截面上一点的应力,围绕该点取一个微面积DA,如图。在这个微面积上内力系的合力为DF,由于这个面积足够小,我们假设其内力为均匀分布,则可得到其平均应力,再取平均应力的极限,可得到该点的总应力或全应力,总应力的方向随着所取点的位置的变化而变化,显然总应力是矢量,其方向与截面的关系是任意的。我们再把总应力分解成两个分量,一个是垂直于截面称为正应力,一个与截面相切称为切应力。
- 平均应力
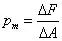
- 全应力(总应力)
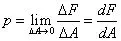
- 全应力分解为: 垂直于截面的应力称为“正应力”,位于截面内的应力称为“切应力”。
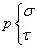
应力的单位:Pa,通常用:MPa、GPa。

三、位移、变形和应变
1. 位移
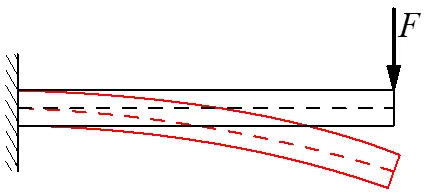
变形前后物体内一点位置的变化,在材料力学中的位移有线位移和角位移,如下图所示悬臂梁,在自由端施加一集中力,梁发生弯曲变形。如果考察某一截面的位移,如自由端的位移,显然截面的形心会产生一个向下的位移,产生了线位移,同时截面的法线方向也产生了变化,即截面发生了转动,产生角位移。
2. 变形
在外力作用下物体尺寸和形状发生改变。
3. 应变
度量构件一点处的变形程度,应变也是针对某“点”而言的。
(1) 线应变(度量物体内一点尺寸的改变程度)。
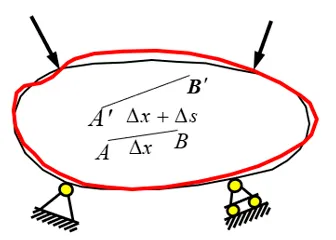
如图我们考察构件内任一点A,在A点附件取任意点B,AB的长为Dx,在外力作用下构件发生变形,A、B两点均产生位移到新的位置,则两点之间的距离变成了Dx+Ds,设在Dx范围内其变形是均匀的,可得平均线应变
我们对上式取极限,可得到A点的线应变
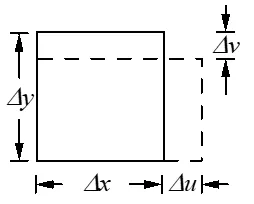
对于平面问题,如图所示一个小矩形,在外力作用线变成虚线所示的矩形(尺寸发生变化),设在Dx,Dy范围内变形是均匀的则有沿x,y方向的平均线应变。
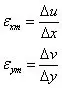
分别取极限得到x、y方向的线应变
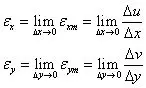
(2) 角应变(度量物体内一点形状的改变程度)也称剪应变或切应变。
定义为直角的改变量。
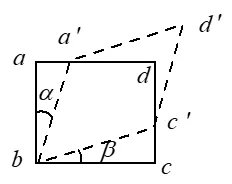
如图ab与bc边互相垂直,变形后为虚线所示,则其角应变为
其严格的表达式为
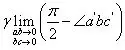
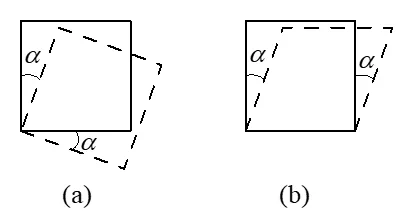
(a)图所示角应变为零(产生了刚体位移,没有发生变形);(b)图所示角应变为a