1. Definition and Characteristics of Plastic Fracture
Plastic fracture, also known as ductile fracture, refers to the fracture process in which significant macroscopic plastic deformation occurs before the fracture. This type of fracture typically occurs under conditions above the material’s yield strength. Compared to brittle fracture, plastic fracture absorbs more energy during the process and is a form of high-energy fracture. In plastic fracture, the material’s fracture toughness is relatively high, so there is often noticeable plastic deformation before fracture, absorbing a significant amount of energy.
2. Basic Concept of J-Integral
The J-integral, introduced by J.R. Rice in 1968, is a path-independent energy line integral used to analyze strain concentration at the crack tip. The J-integral can quantitatively characterize the intensity of the stress-strain field at the crack tip and can be experimentally measured. It is an important fracture parameter in elastoplastic fracture mechanics. In elastoplastic materials, the J-integral includes not only the elastic strain energy but also the plastic deformation energy, allowing for a more comprehensive description of the energy state near the crack tip.
3. Physical Significance and Applications of J-Integral
The physical significance of the J-integral lies in its ability to describe the intensity of the strain field at the crack tip and its association with the material’s fracture toughness. When the value of the J-integral reaches the material’s critical value, Jc, the crack will start to propagate. This critical value, Jc, is referred to as the material’s fracture toughness. In engineering applications, measuring the J-integral can predict the material’s fracture behavior, helping assess the safety and reliability of structures.
- Path Independence of J-Integral: A key feature of the J-integral is its path independence. This means that as long as the path encircles the crack tip and does not intersect the crack, the value of the J-integral will not change. This property simplifies the calculation and experimental measurement of the J-integral, as any convenient path can be chosen for the calculation.
4. Calculation Methods for J-Integral
4.1 Theoretical Foundation and Definition
The calculation of the J-integral is based on its theoretical definition, which is the energy release rate along a closed path around the crack tip. According to Rice’s theory, the J-integral is defined as:
J=\oint_{\Gamma }^{} \left ( Wdy-T_{i}\frac{\partial _{_{u_{i} } } }{\partial _{_{u_{x} } }}ds \right )
Where W is the strain energy density, Ti is the traction vector acting on the integration path, ui is the displacement vector, and Γ is the closed path around the crack tip.
4.2 Numerical Calculation Method
In practical applications, the numerical calculation of the J-integral is typically performed using the Finite Element Method (FEM). By placing finite element meshes around the crack tip, the stress and displacement fields can be calculated, and then the J-integral can be determined. The steps include:
- Create a crack model and mesh the domain.
- Apply boundary conditions and loadings.
- Calculate stress intensity factors and displacement fields.
- Use numerical integration techniques, such as Gaussian integration, to calculate the J-integral.
Currently, ANSYS uses a domain integral method to calculate the J-integral. This method is less sensitive to mesh density at the crack tip, providing stable results with high adaptability for calculating J-integrals in 2D, 3D, and for various crack types.
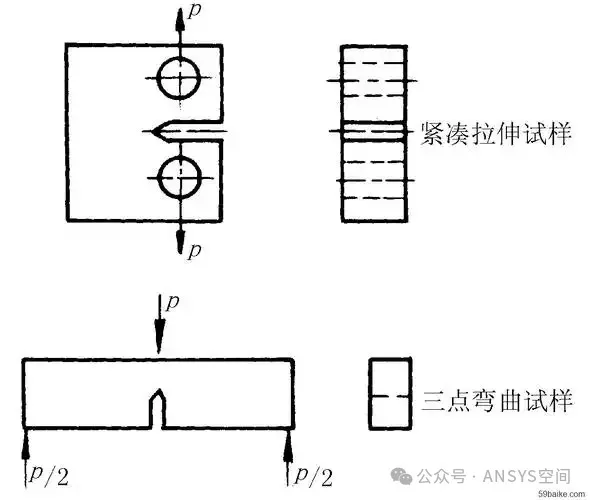
5. Experimental Measurement Methods
Experimental determination of the J-integral typically involves crack propagation experiments, such as Compact Tension (CT) tests or Three-Point Bending (3PB) tests. During the experiment, the displacement field and load response at the crack tip are measured to calculate the J-integral. The steps include:
- Design and fabricate standard specimens.
- Apply loading and record the load-displacement curve.
- Measure the displacement field at the crack tip using techniques like Digital Image Correlation (DIC).
- Use the experimental data to calculate the J-integral.